Конспект урока по информатике в десятом классе.

Тема: «Графы и сети».

Тип урока: комбинированный

Цели урока:

образовательная:

проверка домашнего задания: фронтальный опрос по пройденному материалу, рассмотреть виды графов на примерах, сформировать навыки построения графов

развивающая:

расширить знания учащихся об информационных моделях на графах, развитие коммуникативных способностей, умение анализировать

воспитательная:

воспитывать внимание, сообразительность, умение самостоятельно работать

План урока:

1. Организационный момент.
2. Постановка целей урока.
3. Актуализация прежних знаний: фронтальный опрос по пройденному материалу, проверка домашнего задания.
4. Изучение нового материала: рассмотреть виды графов на примерах.
5. Подведение итогов урока, постановка домашнего задания

Ход урока:

1.Организационный момент.

2.Постановка целей урока.

3.Актуализация прежних знаний.

   а)Фронтальный опрос по пройденному материалу

   1)Что такое граф? Из чего он состоит?

   2)Какой граф называется неориентированным?

   3)Что такое сеть?

   4)Какие характерные особенности имеет сеть?

   б)Проверка домашнего задания.

   Задача 1. Задача о перестановке четырех коней.

Алгоритм перестановки коней

Действие, производимое исполнителем, – это одно перемещение какого-нибудь коня на доступную клетку поля. Запись действий формализируем: сначала обозначим поле, с которого надо переставить коня, потом нарисуем стрелку, а затем обозначим поле, на которое надо поставить коня. Один из возможных алгоритмов имеет вид:

Вывод: таким образом, с помощью неориентированного графа мы рассмотрели информационную модель алгоритма перестановки коней.

4.Изучение нового материала

    Пример 1.

    А теперь рассмотрим другой пример графа, изображенно­го на рис. 1

Этот пример относится к медицине. Известно, что у раз­ных людей кровь отличается по группе. Существуют четыре группы крови. Оказывается, что при переливании крови от одного человека к другому не все группы совместимы.

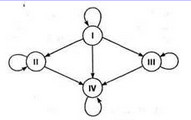
Рис. 1.

Граф на рис. 1 показывает возможные варианты переливания крови. Группы крови — это вершины графа с соответствую­щими номерами, а стрелки указывают на возможность пере­ливания одной группы крови человеку с другой группой крови. Например, из этого графа видно, что кровь 1-й груп­пы можно переливать любому человеку, а человек с первой группой крови воспринимает только кровь своей группы. Видно также, что человеку с 4-й группой крови можно пере­ливать любую, но его собственную кровь можно переливать только в ту же группу.

Связи между вершинами данного графа несимметричны и поэтому изображаются направленными линиями со стрел­ками. Такие линии принято называть дугами (в отличие от ребер неориентированных графов). Граф с такими свойства­ми называетсяориентированным. Линия, выходящая и вхо­дящая в одну и ту же вершину, называется петлей. На рис. 4 присутствуют четыре таких петли.

Пример 2.

Другим знакомым вам примером ориентированного графа являются блок-схемы алгоритмов. Блок-схема алгоритма представляет собой граф процесса управления некоторым исполнителем. Блоки — вершины этого графа — обознача­ют отдельные команды, которые отдаются исполнителю, а дуги указывают на последовательность переходов от одной команды к другой.

На рис.2 представлена блок-схема управления компью­тером для решения следующей задачи: даны значения трех переменных величин: А, В, С. Следует найти наибольшее из них, присвоить его переменной МАХ и вывести на экран.

В блок-схемах используются вершины разных типов, обо­значающие разные команды:  прямоугольник  —  команда присваивания; ромб — команда выбора пути продолжения алгоритма по результату проверки условия; параллелог­рамм — команда ввода или команда вывода; овал — начало или конец исполнения алгоритма. Здесь тоже можно гово­рить о пути прохождения графа в ходе выполнения алгорит­ма. Любой путь начинается от вершины начала и заканчива­ется выходом на вершину конца. Внутри же путь может быть разным в зависимости от исходных данных.

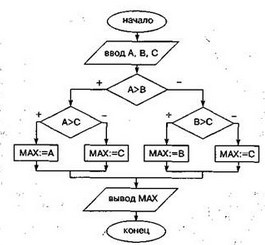
Рис. 2. Блок-схема — ориентированный граф

Работа в классе.

Задача 2. Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют взаимоотношения: дружат – Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша. Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что секрет станет известен кому то другому?

5.Подведение итогов урока. Постановка домашнего задания.