Конспект урока по информатике в десятом классе.

---

Тема: «Графы и сети».

Тип урока: комбинированный

Цели урока:

образовательная:

сформировать у учащихся понятие «граф», познакомить с видами графов, сформировать навыки построения графов

развивающая:

расширить знания учащихся об информационных моделях на графах, развитие коммуникативных способностей, умение анализировать

воспитательная:

воспитывать внимание, сообразительность, умение самостоятельно работать

План урока:

1. Организационный момент

2. Постановка целей урока

3. Актуализация прежних знаний, практическая работа

4.  Изложение нового материала – введение понятия «граф»

5. Постановка домашнего задания и подведение итогов урока

Ход урока:

1.Постановка целей урока.

2.Практическая работа на тему «Модели и система».

   Работа с карточками:

    1. Что такое модель? Приведите примеры моделей.

     2. Начертите схему, какие бывают модели, приведите примеры.

     3. В чем состоит задача системного анализа?

3.Изложение нового материала.

   Данные, используемые в любой информационной модели, всегда определенным образом упорядочены, структурированы. Иначе можно сказать так: данные, на которых базируется информационная модель представляет собой систему со всеми характерными признаками – элементным составом, структурой. Рассмотрим один из основных способов описания структур данных: графы.

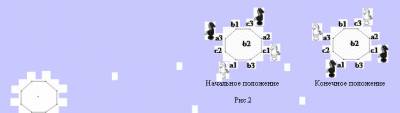
Задача 1. Задача о перестановке четырех коней. Исполнитель – Конюх. Напишите алгоритм (для исполнителя Конюха) перестановки коней из начального (исходного) положения в конечное (целевое) (рис.1).

 

Рис.1

   Конь перемещается за один ход либо на два поля по вертикали и одно поле по горизонтали, либо на два поля по горизонтали и одно по вертикали (буквой «Г»). Конь может перепрыгивать через стоящие на его пути другие фигуры, но может перемещаться (ходить) в нашей задаче только на свободные поля.

Решение. Каждой клетке доски сопоставим точку на плоскости, и если из одной клетки можно попасть в другую ходом коня, то соединим соответствующие точки линией, получим граф (рис. 2)

Рис.2

Начальная и конечная расстановки коней изображены на рисунке 2.

Написание алгоритма перестановки коней для исполнителя Конюха становится очевидным.

Алгоритм перестановки коней

Действие, производимое исполнителем, – это одно перемещение какого-нибудь коня на доступную клетку поля. Запись действий формализируем: сначала обозначим поле, с которого надо переставить коня, потом нарисуем стрелку, а затем обозначим поле, на которое надо поставить коня. Один из возможных алгоритмов имеет вид:

 

 

   Введение понятия графа.

Информация о некотором реальном объекте может быть представлена по-разно­му. В разговорной речи мы используем словесное (вербаль­ное) представление информации. Вот, например, словесное описание некоторой местности: «Наш район состоит из пяти поселков: Дедкино, Бабкино, Репкино, Кошкино и Мышкино. Автомобильные дороги проложены между: Дед-ййно и Бабкино, Дедкино и Кошкино, Бабкино и Мышки­но, Бабкино и Кошкино, Кошкино и Репкино». По такому описанию довольно трудно представить себе эту местность. А представьте себе, что поселков не 5, а 25! Все гораздо по­нятнее становится из схемы.

   Это не карта местности. Здесь не выдержаны направле­ния по сторонам света, не соблюден масштаб. На этой схеме отражен лишь факт существования пяти поселков и дорож­ной связи между ними. Такая схема называется графом.

   Граф отображает элементный состав системы и структуру связей.

   Составными частями графа являются вершины и ребра. Здесь вершины изображены кружками — это элементы сис­темы, а ребра изображены линиями — это связи (отноше­ния) между элементами. Глядя на этот граф, легко понять структуру дорожной системы в данной местности.

Построенный граф позволяет, например, ответить на во­прос: через какие поселки надо проехать, чтобы добраться из Репкино в Мышкино. Видно, что есть два возможных пути; обозначим их так:

1)Р — К — Б — М

2)Р - К — Д — Б — М

Очевидно, первый путь более выгодный, потому что он короче. Однако, если по какой-то причине дорога между К и Б окажется не проезжей (идут ремонтные работы или занес­ло снегом), то единственным остается второй путь. Граф на рис. 3.4 еще называют сетью.

   Для сети характерна возможность множества различ­ных путей перемещения по ребрам между некоторыми парами вершин.

   Для сетей, также характерно наличие замкнутых путей, которые называются циклами. На рис. 3 имеется цикл: К — Д — Б — К. Кстати, термин «дорожная сеть» исполь­зуется и в разговорной речи. И чем такая сеть гуще, тем лучше для сообщения, поскольку появляется множество различных вариантов проезда.

Граф, изображенный на рис., является неориентиро­ванным графом. На нем каждое ребро обозначает наличие дорожной связи между двумя пунктами. Но дорожная связь действует одинаково в обе стороны: если по дороге можно проехать от Б к М, то по ней же можно проехать и от М к Б. Такую связь еще называют симметричной.

 

А теперь рассмотрим другой пример графа, изображенно­го на рис. 4

Этот пример относится к медицине. Известно, что у раз­ных людей кровь отличается по группе. Существуют четыре группы крови. Оказывается, что при переливании крови от одного человека к другому не все группы совместимы.

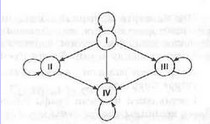
   Граф на рис. 4 показывает возможные варианты переливания крови. Группы крови — это вершины графа с соответствую­щими номерами, а стрелки указывают на возможность пере­ливания одной группы крови человеку с другой группой крови. Например, из этого графа видно, что кровь 1-й груп­пы можно переливать любому человеку, а человек с первой группой крови воспринимает только кровь своей группы. Видно также, что человеку с 4-й группой крови можно пере­ливать любую, но его собственную кровь можно переливать только в ту же группу.

Связи между вершинами данного графа несимметричны и поэтому изображаются направленными линиями со стрел­ками. Такие линии принято называть дугами (в отличие от ребер неориентированных графов). Граф с такими свойства­ми называетсяориентированным. Линия, выходящая и вхо­дящая в одну и ту же вершину, называется петлей. На рис. 4 присутствуют четыре таких петли.

4.Подведение итогов урока, постановка домашнего задания.